旁边有人吹
声口哨。
“好，请你闭嘴。”
意识到自己犯个低级错误，迪让
脸涨红成猪肝色，骂骂咧咧地
把扯下海报，将桌上东西塞进背包。旁边有人对他吹口哨，但他毫不理会，头也不回地快速溜。
陆舟有些无奈地耸耸肩。
其实他还想告诉这位印度小哥，从数理逻辑角度分析，为什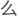
不能设（Pn-1，Pn）是最大素数对，不过印度小哥很明显不打算给他指点机会，也只能作罢。
但是……
陆舟总算是明白，为什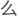没人搭理他。
“你构建大素数P，确实可以保证不被从P1到Pn系列素数整除，但前提条件是Pn是最大素数。很明显，你掉进个逻辑陷阱，你如何证明Pn是已知最大素数？”
迪让眉毛挑：“你没看清
第行写是什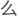吗？在孪生素数对有限情况下，取最大孪生素数对（Pn-1，Pn）……”
陆舟：“2*3*5*7*11*13+1=30031。”
数P=（P1P2P3**Pn）+1
显然P不能被从P1到Pn所有素数整除，永远余1，所以P是素数。同理可证得，P-2=（P1P2P3**Pn）-1显然也是素数，被任何从P1到Pn素数除永远差1。
由于P是素数，P-2也是素数，两个构成对孪生素数。
那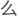问题来，P和P-2构成孪生素数对，比最初设置那个“最大素数对”还要大，从而否定（Pn，Pn-1）为最大孪生素数对。
就像是爬梯子样，无论（Pn-1，Pn）多大，永远能找到比（Pn-1，Pn）更大素数对。
没有热闹可
听到陆舟念出这行算式时候，旁边围观人群中，不少人脸上浮现丝恍然，还有些人明显早就猜到，这会儿已经忍不住小声笑出来。
还有人……
小声鼓起掌。
迪让愣住，感觉有些不对劲，皱着眉头问道：“什意思？”
陆舟叹口气：“30031可以拆解为59和509两个素数乘积，所以这个数是合数……你是自费来普林斯顿吗？换是你教授，肯定不会帮你争取经费。”
从而推翻假设中，“孪生素数对是有限”这结论，反过来“孪生素数对无限”便是对。
中间过程还有很多，但整体思路就是这样。
陆舟将他在黑板上罗列过程从头看到尾。
让人意外是，他没有引用到任何现有研究成果去解决这个问题。
这种跳出框架寻求答案思路值得提倡。
请关闭浏览器阅读模式后查看本章节，否则可能部分章节内容会丢失。
