“想像
个不分内外侧
泳圈，那就是克莱因壶。”
“…………”
七美见
苦着脸，不禁笑着摇头：
“怎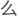
说明才好。”
“从开始地方开始，在结束地方结束。”
“对，克莱因壶即是四次元莫比乌斯带。”
“四次元莫比乌斯带……”皱起眉，“那又是什？”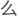
“莫比乌斯带中段有个转折，若沿表面画线，会不知不觉绕到背面，这你知道吧？”
“嗯，莫比乌斯带表面与背面是相连通。”
“没错，这意味着莫比乌斯带没有表里分别。表就是里，里就是表。将此概念立体化，便是克莱因壶。想想，你看过泳圈吧？”
“技术人员都称其为‘克莱因壶’，上市后应该会另外正式取名。那装置外形其实不像壶，反倒接近蓄水塔。”
“拓扑学‘克莱因壶’？”
“拓扑学？”
困惑地望着七美。
“你没听过？”
“这简直不可思议。”
坐在咖啡厅内靠窗桌位，七美开口前，吸干杯里最后点冰可可。
向七美坦白切。从伊普西隆制造K2，以《大脑病变》为脚本，开发出划时代虚拟游戏，梨纱被聘为测试员，每天必须进入游戏三次，及至梶谷孝行谎言、今天偷听到英语通话。虽尽量精简，然而说完时外面天色已暗。
七美看着，不住摇头。
“相信梨纱并非主动辞职，因为伊普西隆早在前天便安排好递补人选。不过，即使她是遭到开除，也没道理就此销声匿迹。”
七美忍不住笑出声。“晓得有点难，不过你试想
“泳圈？”
“旱鸭子进泳池时必备物品。”
“啊，那当然。”
“泳圈包住空气部分是内侧，摸得到是外侧。”
“嗯。”
“那是？”
“Topology，似乎又叫位相几何学，在书上看过。总之是数学领域之，和几何学相关。”
“哦，你对这方面有研究？”
“算不上，只是有点兴趣，曾找资料来读。复杂理论不懂，但拓扑学真很有意思，举个例子，你晓得莫比乌斯带吗？”
“你是指，把长带尾端翻面后，两头黏在起环？”
“小肩包为何出现在房里，无法解释，但她真没回来。”
点点头。沉默片刻，想续点冰咖啡时，七美悄然抬头，迷惘地问：
“K2是什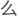缩写？既然有K2，是不是还有个K1？”
“装置名为‘KLEIN-2’，所以简称K2。至于K1，则是在美国开发，日本并未引进。”
“KLEIN-2……”
请关闭浏览器阅读模式后查看本章节，否则可能部分章节内容会丢失。
